原理介绍
Greedy:贪心算法,又称贪婪算法,人要活在当下,看清楚眼前,这种思想就是贪心思想。是指在对问题求解时,总是做出当前最好的选择,不从整体最优上加以考虑。也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。
核心思想
贪心选择
贪心选择指原问题的整体最优解可以通过一系列局部最优的选择得到。应用同一规则,将原问题变为一个相似的但规模更小的子问题,而后的每一步都是当前最佳的选择。这种选择依赖于已做出的选择,但不依赖于未做出的选择。
最优子结构
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题能否可用贪心算法求解的关键。如原问题$S=\lbrace a_1, a_2, a_3, \ldots, a_n \rbrace$,通过贪心选择出一个当前最优解${a_i}$之后,转化为求解子问题$S- \lbrace a_i \rbrace $,如果原问题的最优解包含子问题的最优解,则说明该问题满足最优子结构性质。
经典例题(背包问题)
问题描述
假设山洞里有n个宝物,每种宝物有一定重量w和相应的价值v,背包的装载能力有限,只能运走重量为m的宝物,宝物可以分割,如何使背包运走物品的价值最大?
第一行先输入宝物的数量n,和背包的承载重量m,然后每一行输出一个宝物对应的重量w和价值v(用空格分开)
1 | 6 19 # 宝物数n和背包能装载的重量m |
算法分析
对于普通背包问题,宝物可以分割,当前取得的宝物不会受到后面宝物的影响,如果是0-1背包,即物品不可以分割,当前宝物就会受到后面宝物的影响。假设该问题的最优解为S,拿走当前最优解第i个宝物,现在转换成一个新问题,有n-1个宝物,背包重量为$m-w_i$,可以得到最优解为$S- \lbrace a_i \rbrace$。因此可以使用贪心算法。
该问题有三个思考方向
(1)选择价值最大的宝物装入背包
(2)选择重量最小的宝物装入背包
(3)选择单位重量价值最大的宝物装入背包
选择价值最大的宝物,如果重量也很大,则不是最优解;选择重量最小的宝物,如果价值也很小,则也不是最优解;因此应该选择单位重量价值最大的宝物。
流程图
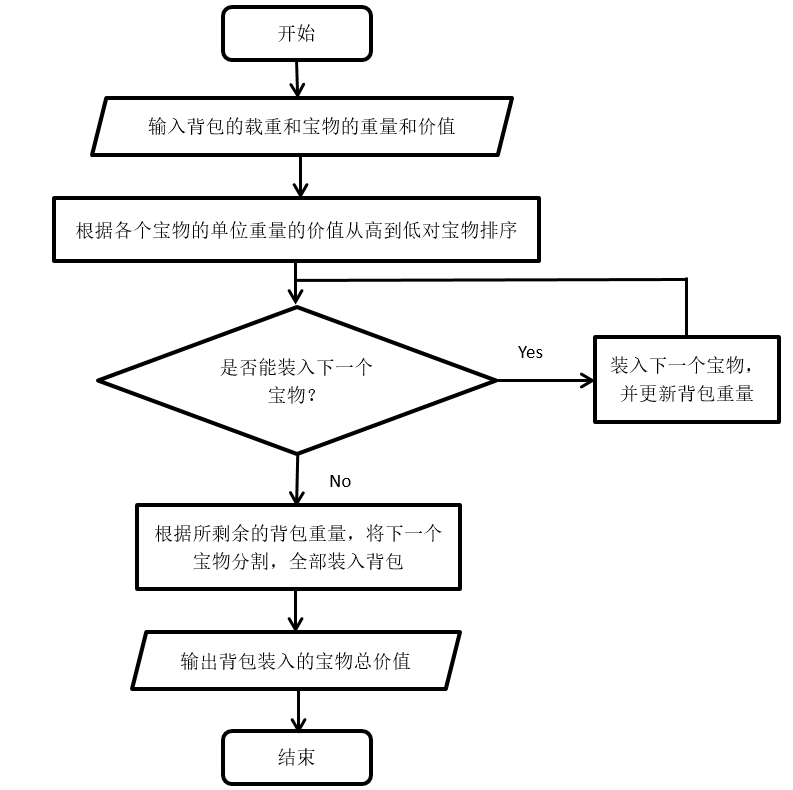
python代码实战
1 | import sys |
代码运行结果
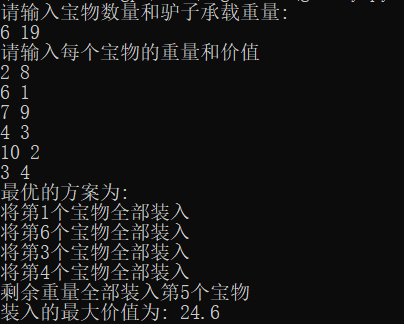
经典例题(最短路径)
问题描述
现有一个景点地图,有n个城市,m条路径(路径是有向的,即来回的距离不同),假设从某一结点出发,求到其他各个结点的最短路径。
第一行先输入城市数n,第二行输入总路径数m,然后每一行输入A市,B市,以及A到B的距离(用空格分开),最后输入起始位置和目的地位置。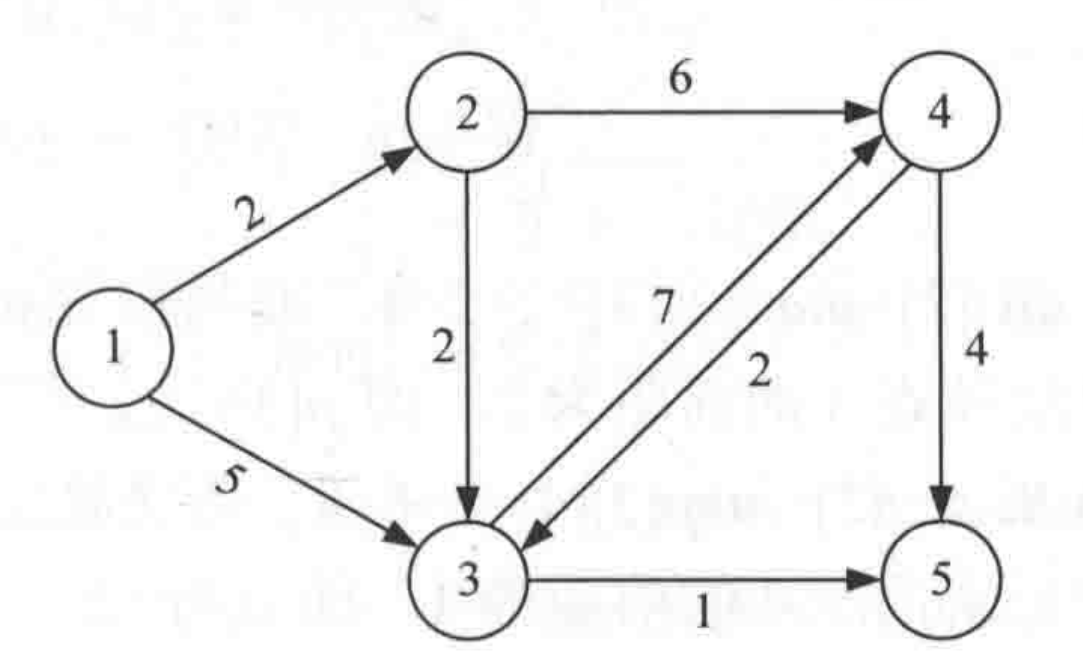
1 | 5 # 城市数n |
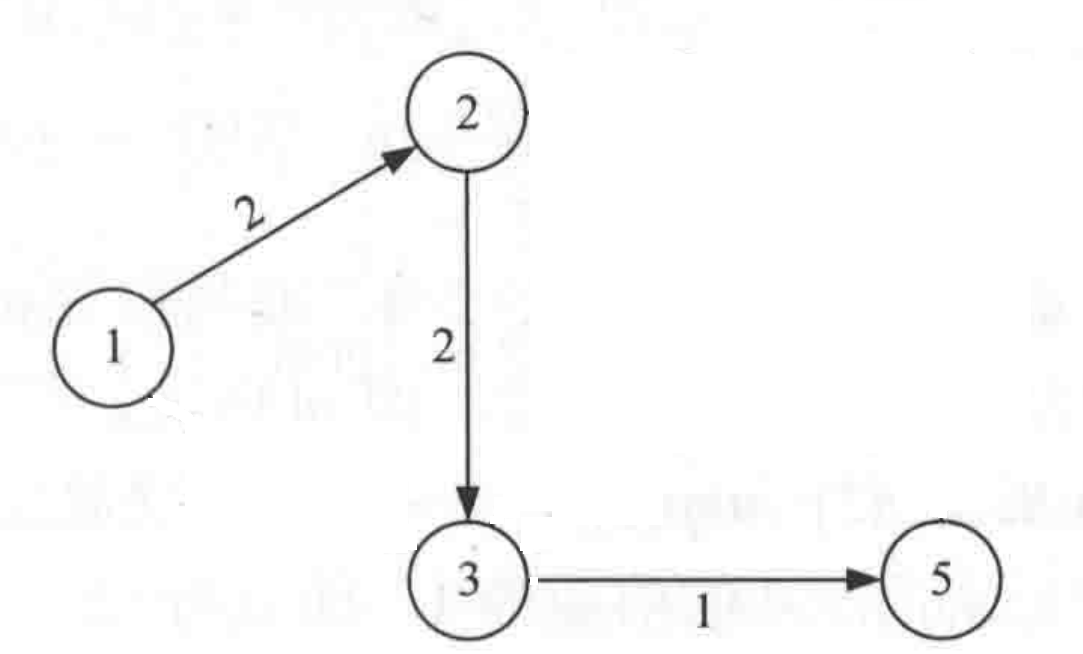
算法分析
最短路径算法是1959年由荷兰图灵奖得主Edsger Wybe Dijkstra(艾兹格·迪科斯彻)提出的,从起始点开始,逐渐增加结点数,依次求出源点到各个定点的最短路径,直到求出目标结点。
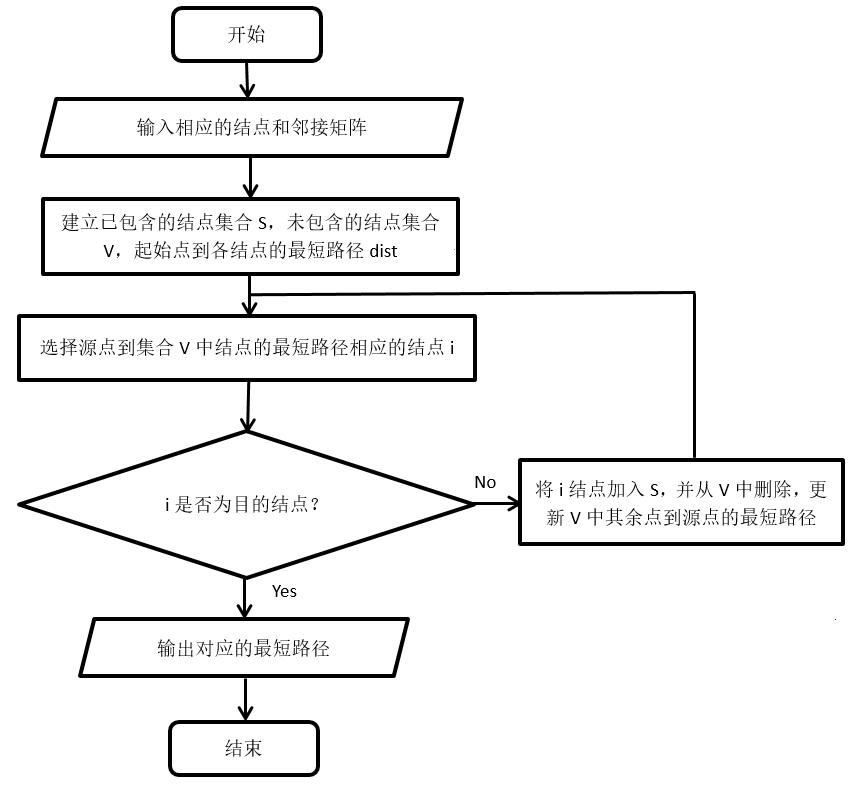
首先建立一个数组dist,存放从源点到各点的最短路径,列表S,代表已经包含的结点数,初始值为空。S中的结点,代表从源点到该点的最短路径已确定。列表V,代表没有包含的结点数,初始值为全部结点,然后从这些结点中寻找距离源点最近的结点(贪心算法)。假如找到某一点i,说明从源点通过S,到达i的最短路径为dist[i],将i加入S,并从V中剔除。更新V中其余的点到源点的最短路径,即检查其余各点是否可以通过i点到达源点。
流程图
python代码实战
1 | import sys |
代码运行结果

经典例题(最小生成树)
问题描述
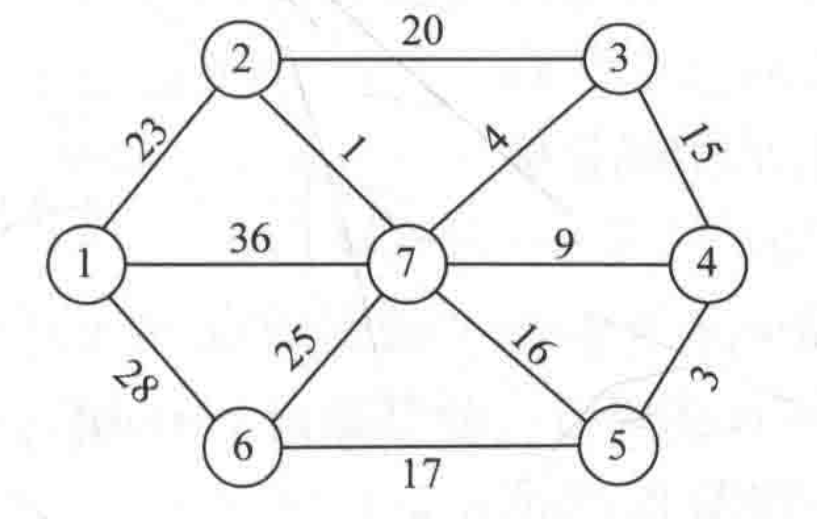
现有一个学校,下面有n个学院,m条路经(路径是无向的,即来回的距离相同)现在设计一条网络布线,将各个学院联通起来,问如何设计可以使费用最少。
第一行先输入结点数n和边数,然后每一行输入A,B,以及A到B的距离(用空格分开),最后输入起始位置。
1 | 7 12 #输入结点数和边数 |
算法分析
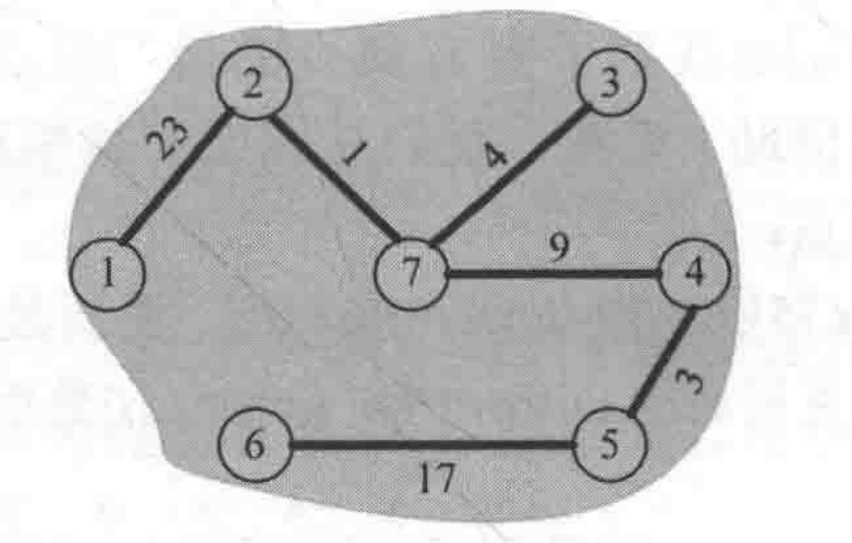
最小生成树算法是1957年由Robert C. Prim(普里姆)提出的,和dijkstra算法类似,从起始点开始,逐渐增加结点数,依次求出每一步的最小生成树,直到包含所有结点。
首先建立一个列表S,代表已经包含的结点数,初始值为空。S中的结点,代表从源点到该点的最短路径已确定。列表V,代表没有包含的结点数,初始值为全部结点。建立一个数组cost,存放从V中结点到S中最近邻点的距离,然后从这些距离中寻找最短的距离(贪心算法)。假如找到某一点i,将i加入S中,说明此时S是最小的生成树,并将i从V中剔除。更新V中其余的结点通过i结点到达S中结点的最近邻的路径。
流程图

python代码实战
1 | import sys |
代码运行结果

算法总结
贪心算法相对简单,代码易于实现。但是由于其只关注于当前的最优解,很难得到全局最优解,不符合人类的思维习惯,因此在日常生活中,很少见到贪心算法处理的问题。